The Distributive Property and Order of Operations Review
What is the distributive holding? Likewise known as the distributive police force of multiplication, it'southward one of the virtually unremarkably used properties in mathematics.
When you distribute something, you are dividing information technology into parts. In math, the distributive property helps simplify difficult issues because it breaks downwardly expressions into the sum or difference of two numbers.
Co-ordinate to this principle, multiplying the total of 2 addends by a number volition give us the exact same result as multiplying each addend individually by the number and and then calculation them together.
Understanding distributive property
For expressions in the grade of a(b+c), the distributive property shows us how to solve them by:
- Multiplying the number immediately exterior parentheses with those inside
- Adding the products together
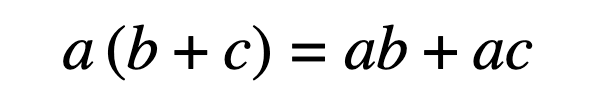
What about PEMDAS? What happened to first evaluating what'south inside parentheses?
If your students are wondering why you lot aren't following the order of operations you've taught them in the by, they're not incorrect.
However, when algebraic expressions accept parentheses containing variables — a quantity that may change within the context of a mathematical problem, usually represented by a single letter — performing that operation isn't possible.
Distributive belongings of multiplication over addition
Regardless of whether you use the distributive belongings or follow the order of operations, you'll arrive at the same answer. In the first example beneath, we but evaluate the expression according to the social club of operations, simplifying what was in parentheses commencement.
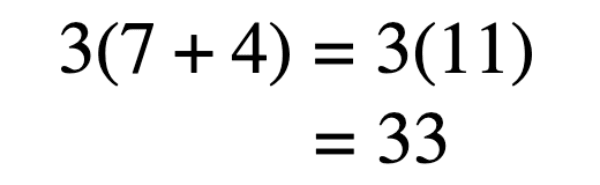
Using the distributive police, we:
- Multiply, or distribute, the outer term to the inner terms.
- Combine similar terms.
- Solve the equation.
Let's use a existent-life scenario equally an example of the distributive belongings.
Imagine 1 student and her two friends each take 7 strawberries and four clementines. How many pieces of fruit do all three students take in full?
In their tiffin numberless — or, the parentheses — they each have 7 strawberries and iv clementines. To know the total number of pieces of fruit, they demand to multiply the whole thing past 3.
When y'all break it down, y'all're multiplying 7 strawberries and iv clementines by 3 students. And then, you end up with 21 strawberries and 12 clementines, for a total of 33 pieces of fruit.
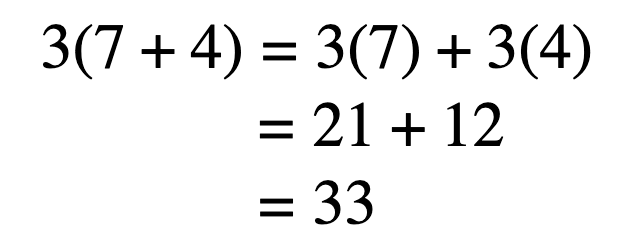
Distributive property of multiplication over subtraction
Similar to the performance above, performing the distributive belongings with subtraction follows the same rules — except y'all're finding the deviation instead of the sum.
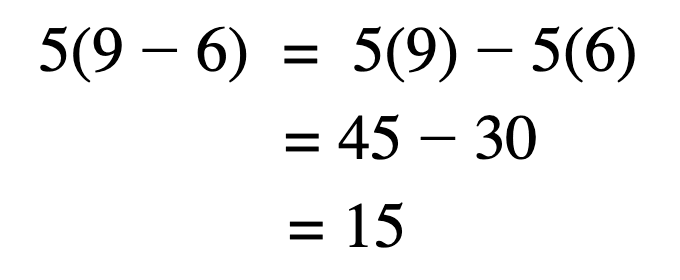
Note: Information technology doesn't matter if the performance is plus or minus. Keep whichever one is in the parentheses.
Distributive property with variables
Retrieve what we said about algebraic expressions and variables? The distributive property allows us to simplify equations when dealing with unknown values.
Using the distributive law with variables involved, we tin isolate x:
- Multiply, or distribute, the outer term to the inner terms.
- Combine like terms.
- Arrange terms so constants and variables are on opposite sides of the equals sign.
- Solve the equation and simplify, if needed.
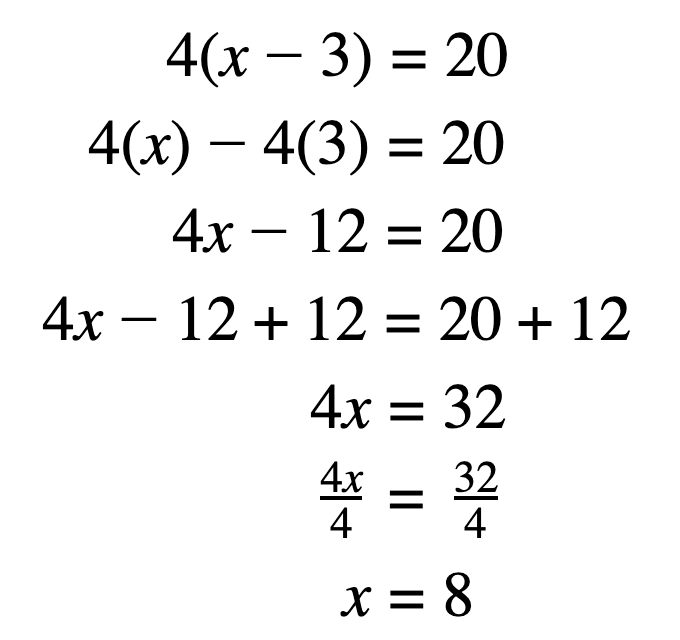
Annotation: When isolating variables (encounter step three) what yous do to one side you must do to the other. In order to eliminate 12 on the left side, you must add twelve to both the left and right sides. The same goes for multiplication and division: to isolate x, split each side by 4.
Distributive property with exponents
An exponent is a autograph notation indicating how many times a number is multiplied past itself. When parentheses and exponents are involved, using the distributive holding can make simplifying the expression much easier.
- Expand the equation.
- Multiply (distribute) the starting time numbers of each set, outer numbers of each ready, inner numbers of each set up, and the last numbers of each set.
- Combine like terms.
- Solve the equation and simplify, if needed.
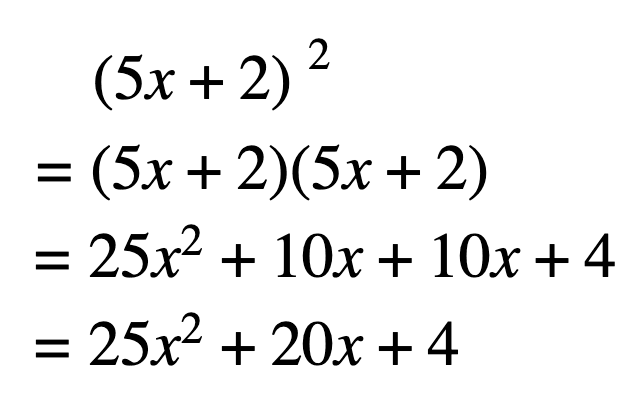
Note: For step two, use the FOIL (first, outer, inner, terminal) technique to distribute each expression.
Distributive property with fractions
Solving algebraic expressions with fractions looks more complicated than it is. Follow the steps outlined beneath to run into how it'southward done.
Hopefully, this pace-by-stride process helps your students understand how and why the distributive property can come in handy when simplifying fractions and complex numbers.
- Identify the fractions. Using the distributive property, you'll eventually turn them into integers.
- For all fractions, notice the lowest common multiple (LCM) — the smallest number that both denominators can fit neatly into. This will allow you to add fractions.
- Multiply every term in the equation past the LCM.
- Isolate variables calculation or subtracting like terms on both sides of the equals sign.
- Combine like terms.
- Solve the equation and simplify, if needed.
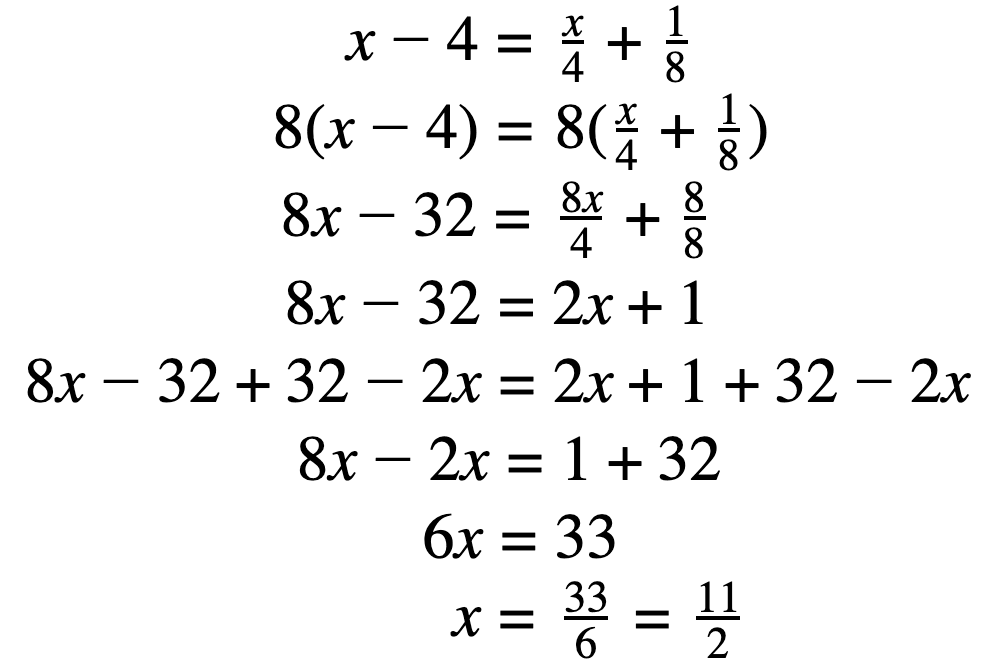
Note: In steps two and three, we find the LCM and use it to multiply the fractions in order to simplify and go rid of them. Need a quick refresher? See our web log mail on how to multiply fractions.
A multifariousness of backdrop
Apart from distributive holding, at that place are other ordinarily used properties such equally the associative holding and Commutative holding.
Let'due south look at the associative belongings:
The associative holding refers to grouping elements together. This dominion states that how numbers (or whole numbers) are grouped inside a math problem will not change the production.
Example in add-on:
a + (b +c) = (a + b) + c or two + (3 + four) = (2 + three) + four
Example in multiplication:
5×4×ii = (5 x 4) x ii = 20 ten 2 = 40
This property works with multiplication, add-on, subtraction, and division.
Exploring distributive belongings in different means
one. Prodigy
Prodigy is an adaptive, game-based learning math platform loved by more than one million teachers 150 one thousand thousand students effectually the world! It offers curriculum-aligned content from every major math topic in 1st to 8th grade, including how to:
- Utilise the distributive property to expand and solve expressions
- Fill up in the missing numbers in equivalent expressions using the distributive holding
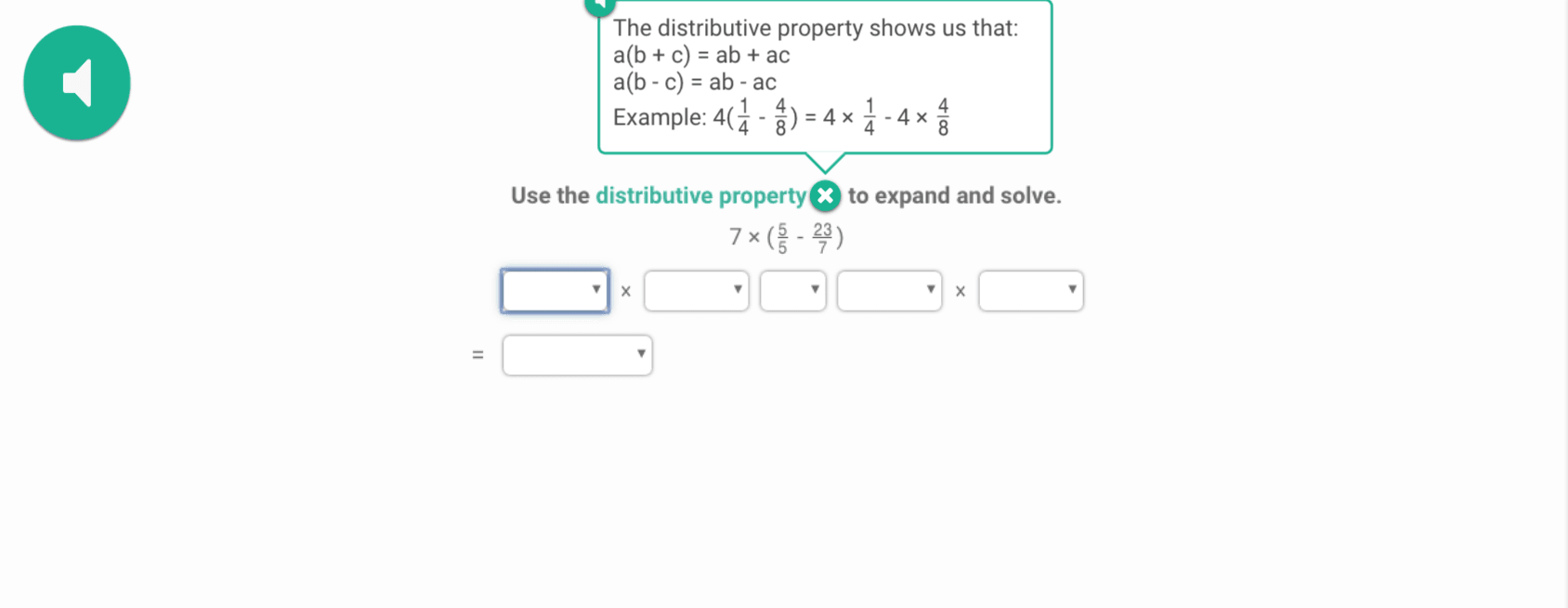
Using Prodigy Math Game tin can help students larn and do math across fact fluency and into DoK levels 2 and three. With questions like the i to a higher place, students volition have a blast as they practice the distributive holding.
Interested in supplementing math lessons with an engaging game-based learning platform and powerful teacher tools?
2. Word problems
The distributive property may not see applicable to everyday life, only let's meet it in action through some word problems!
Liam has diverse taste in music. Scrolling through the music on his phone, Liam'southward friends find songs from 3 different genres: popular, metal, and country. At that place are half-dozen times every bit many metal songs as there are popular songs, and eleven times as many country songs as there are pop songs. If x represents the number of pop songs, what is the total number of songs Liam has on his phone? Write an expression. Simplify.
To become the number of metallic songs, multiply the number of pop songs by five — 5x. To go the number of country songs, multiply the number of pop songs past xi — 11x. Since you know ten is the number of pop songs, you lot can write the expression as:
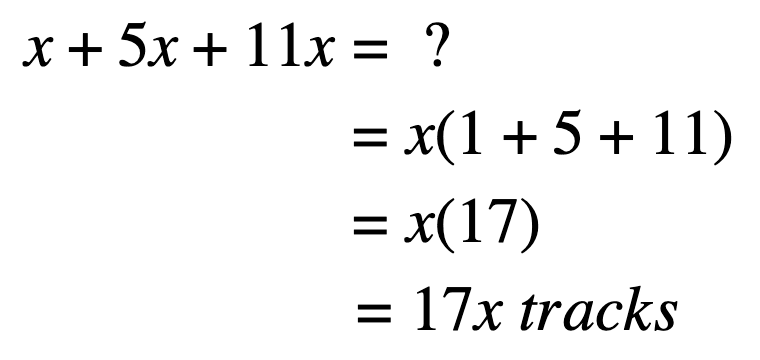
The schoolhouse'south soccer coach is providing his squad with new uniforms: a jersey, a pair of shorts, and shin guards. One jersey costs $15, one pair of shorts costs $11, and a set of shin guards costs $8.
How much does each compatible cost per squad mate? Write an expression and simplify.
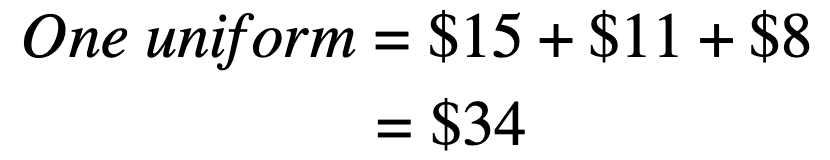
How much will it cost in total if the team has 11 players? Write an expression and simplify.
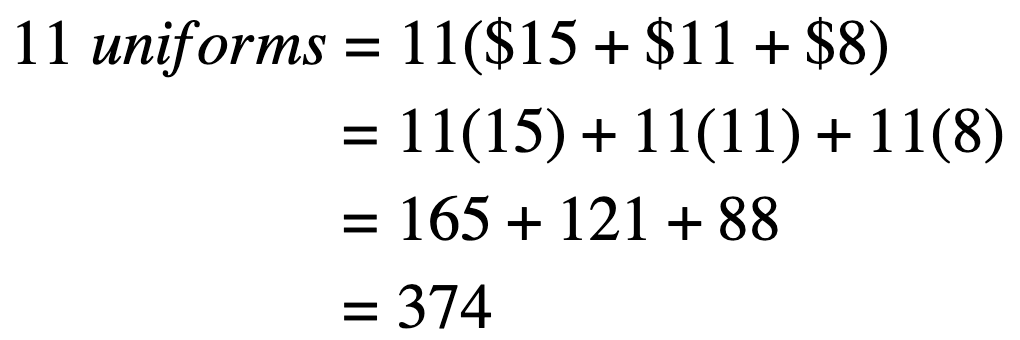
iii. Arrays
Visual or hands-on manipulatives aid students make sense of math and concretize abstract concepts. They're especially helpful for deepening your students' understanding of the distributive belongings.
Use objects, pictures, numbers — anything! — in rows and columns as a useful style to represent mathematical expressions like 4x5 and 5x9. Check out the case below on Indulgy:

Past breaking downward expressions into bite-sized pieces, students tin can tackle larger and more than challenging math problems. That's where distributive property helps.
If a child has trouble answering 45, utilize smaller arrays and rewrite the expression equally 4(three+2) or 4(3)+iv(two). That'due south four rows of 3 plus iv rows of 2, which is the same as an array of iv rows of v.
Final thoughts on the distributive property
As one of the most commonly used properties, information technology's of import to larn how to perform and utilize the distributive property. Without it, clearing the parentheses wouldn't be possible.
By incorporating EdTech resources, arrays, or math word problems, students should see the hands-on, practical applications of the distributive property.
Did one example work more effectively to appoint students and deepen their understanding? There's just i mode to find out — requite them a try!
Prodigy Math Game is a game-based learning platform for math that'south easy to utilize for educators and students alike. Aligned with curricula across the English language-speaking world, your costless teacher account gives yous access to tools that help with differentiation, motivation and assessments.
Source: https://www.prodigygame.com/main-en/blog/distributive-property/
0 Response to "The Distributive Property and Order of Operations Review"
Enregistrer un commentaire